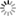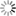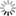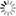LASCA with autoencoders
A sequence of steps implements the LASCA strategy
It is known that, in general, population based (PB) methods, such as Evolutionary Algorithms (EA) like Evolutionary Programming (EP) or Genetic algorithms (GA), or as Particle Swarm Optimization (PSO) or Ant Colony Methods (ACM), used in optimization, exhibit a growingly slow and inaccurate performance with the increase in dimension of the search space where individuals (chromosomes, particles) are defined. This limits the practical application of parallel processing methods in large scale programming problems. However, these problems appear as extremely relevant in a diversity of engineering areas; for instance, in Power Systems it is not at all uncommon to find planning or operation problems with hundreds to tens of thousands of variables.
The original idea explored in the LASCA project is, therefore, to use autoencoder properties to reduce the dimension of the search space, while keeping the solution evaluation accurate so that selection or similar operators may still act and drive the process towards an optimum. This idea can be summarized in the following sequential parts.
Part A
A PB algorithm with individuals (particles) is applied in a seacrh space S. The project adopted EPSO as the reference metha-heuristic for all tests (see the EPSO section). The solutions obtained over a specified number of iterations are stored. Two particles are considered equal if all homologous values are equal for all positions. Moreover, different particles can assume equal fitness values.
The stored solutions are used as a dataset to train an autoencoder. The autoencoder will allow the encoding and decoding of particles between S and a reduced space S'.
Schematic of an autoencoder. A vector in space S is encoded into a reduced space S' by f, and is reprojected (expanded) back to S by f -1.
Part B
The last swarm obtained in part A, evolving in S, will be transferred to S'. The information transferred includes the particles and the corresponding best positions, velocities and weights of inertia, cooperation, memory and perturbation.
The transference of particles and corresponding best positions is made by applying the encoding function corresponding to the 1st half of the autoencoder.
The transference of velocities is made as the difference between the corresponding compressed positions in S and in S'. The transference of weights of inertia, memory and cooperation is made directly.
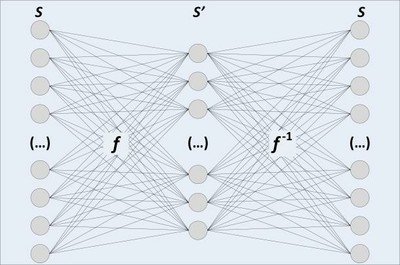
Once the swarm is completely transferred, it starts to evolve in S'. The evaluation of the fitness function would not be possible in S', since the values that particles assume in the reduced space have no physic meaning. Therefore, when such assessment is necessary, the particles are first decoded into , and only then evaluated, as represented in Fig. 3. This procedure ensures that the evolution observed in S' actually corresponds to an improvement on the problem addressed.
Particles evolve in S but the fitness evaluation is made in S' using the decoding function f -1 on the 2nd half of the autoencoder
Part C
Because the autoencoder is just an approximation and not a representation of the exact mappings f <--> f -1, some information will eventually be lost. It is possible then that the exact optimum of the original problem may not be found in S – but if the approximation is good enough, a near optimal solution or, at least, the location of the optimum will be found. Therefore, the launching of an efficient post-optimization search, back in S', is implemented.
This is made by transferring the last swarm obtained in Part B back in S'. This transference includes the same elements and the same procedures described before, now using f -1 corresponding to the 2nd half of the autoencoder.